Illumina

@Lemmi

Die Messung Sulfat habe ich bei 450nm vorgenommen, die Auswertung habe ich dann unter Excel mit der Binom-Funktion erledigt.

Damit habe ich übrigens auch Photometrie und AAS oberhalb des linearen Bereiches, bzw. bei Emissionsspektrometrie generell die
Auswertung vorgenommen. Es ist ein hartnäckiges Vorurteil in vielen Labors, daß oberhalb des linearen Bereiches die Analysen
ungenauer werden. Natürlich muß man die Auswertung anpassen und auch den Bereich nicht übertreiben, alles hat seine Grenzen.

Gruss Römpp63

Bei einer solchen Kristallisation würde ich folgendes Vermuten: Die Nukleationsrate hat irgend eine eigene Konzentrationsabhängigkeit und der restliche Kristallisationsprozess verläuft diffusionskontrolliert. Was wir suchen ist die Zeit, bis die Kristalle so weit gewachsen sind, dass sie sichtbar werden und etwas trüben können.

Eine Auftragung von Konzentration gegen Zeit würde man machen, wenn man bei einer Reaktion z.B. erster Ordnung die Konzentration über einen Zeitraum hinweg gemessen hat. Das hat er aber doch gar nicht getan. Er hat die Zeit gemessen, bis eine gewisse Menge Produkt entstanden ist.

Gehen wir mal davon aus, dass die Reaktion bei doppelter Konzentration doppelt so schnell abläuft (und über die kurzen Zeiträume näherungsweise konstant bleibt, da sich die Bulk-Konzentration durch die geringe, kaum sichtbare Niederschlagsmenge nicht merklich ändert), dann muss bei halber Konzentration die doppelte Zeit benötigt werden. Das bedeutet also, man müsste das Inverse der Zeit gegen die Konzentration auftragen.

1/t ~ [A]

Da kommt aber nichts Gutes bei raus.

Gehen wir aber gar nicht von einer Reaktion erster Ordnung aus, sondern vermuten wir, dass die Kondensationsrate exponentiell mit der Konzentration steigt (eigentlich auch plausibel, denn bei größeren Konzentrationen fällt das ja richtig schlagartig aus), dann hätten wir folgende Proportionalität der Zeit in Abhängigkeit von der Konzentration:

ln(1/t) ~ [A]



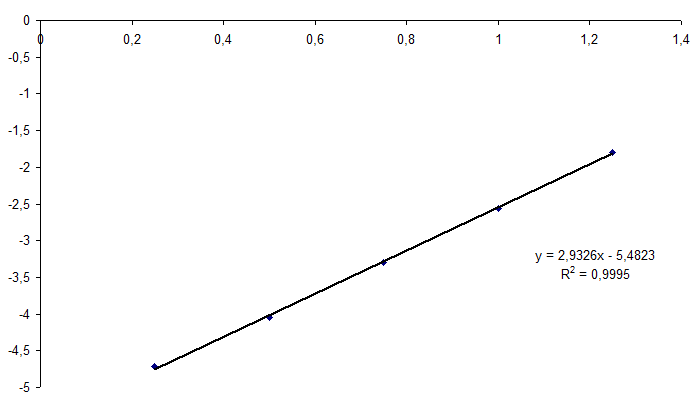
Der sieht zumindest nach einer Geraden aus. Nach so vielen Rechenoperationen ist das aber alles andere als verlässlich, da auf das Bestimmtheitsmaß zu gucken. Ich glaube das ist immer die Frage, welche Fehler man da grade wie in seine Rechnung reinschleift, ob sie gut "konditionieren" oder sich völlig desaströs verstärken.

Es ist ein hartnäckiges Vorurteil in vielen Labors, daß oberhalb des linearen Bereiches die Analysen
ungenauer werden.

Irgendetwas (Kein Sarkasmus, das ist wirklich nur so eine Ahnung) sagt mir, dass man dieses "Vorurteil" mathematisch beweisen kann. Wobei aber "ungenauer" auch beliebig irrelevant schwach sein kann, also mal wieder ein Beispiel dafür, das man aufpassen muss, was man da bewiesen hat.

@xyrolf
Ich kann dir versichern, daß meine jeweiligen Vorgesetzten ebenfalls deiner Meinung waren. Und in Zeiten von ISO9000 und diversen Ablegern
kann man in der Analytik nicht mehr aus der Hüfte schießen. Man muß in jedem Einzelfall die Methode fachgerecht überprüfen und mit Richtig-
keits- plus Standardadditions-Serien sowie Standardabweichung dokumentieren.
Natürlich gibt es Fälle, bei denen oberhalb des linearen Bereiches die Methode schlichtweg nicht mehr richtig funktioniert. Aber wie gesagt, muß
man dies für jede Methode überprüfen.

Wollten sie dich damit kritisieren? Na dann waren sie sicher nicht meiner Meinung.
Wollten sie dir in der Kaffeepause aus Spaß mitteilen, dass sie vermuten, die Gerade sei mathematisch gesehen die optimale Form der Kalibrierkurve, wo Fehler sich am wenigsten auswirken?
Dann waren sie meiner Meinung.

Xyrofl hat geschrieben:Nach so vielen Rechenoperationen ist das aber alles andere als verlässlich, da auf das Bestimmtheitsmaß zu gucken.

Dein R² ist doch dasselbe wie meins. Muss es doch auch sein, oder nicht? Und ich habe gar keine Rechenoperationen gemacht.

Problematischer finde ich eher die Erhebungsmethode der Zeiten. Die Zeit bei der höchsten und niedrigsten Konzentration wurde ja nur geschätzt und nicht gemessen, wenn ich das richtig verstanden habe. Am besten sollte man es so machen, dass man den Versuch "blind" durchführt, um nicht die Werte entsprechend der eigenen Erwartung unbewusst anzupassen. Also am besten die Zeit von einer anderen Person stoppen lassen - oder keine so gleichmäßige Konzentrationsreihe machen, sondern 0,2 - 0,45 - 0,68 - 0,82 mM usw. Und die Uhr am besten auch so umdrehen, dass man den Zeiger nicht sehen kann. So kann man die Ergebnisse nicht unbewusst manipulieren. Aber in diesem Fall sieht es ziemlich eindeutig aus und vermutlich hätte dieses aufwendigere Verfahren auch keine großen Änderungen bei den Zeiten gebracht.

Dein R² ist doch dasselbe wie meins. Muss es doch auch sein, oder nicht? Und ich habe gar keine Rechenoperationen gemacht.

Ist nen bisschen Quatsch, weil das Invertieren nur einen Vorzeichenwechsel darstellt, wenn logarithmiert wird, also eigentlich waren die "vielen Operationen" nur logarithmieren. Aber das kann gewaltig sein, wenn Fehler der Gerade sich exponentiell auswirken.
Es ist schon bei Geraden nicht richtig, von dem Bestimmtheitsmaß auf den Regressionsfehler und die Genauigkeit schließen zu wollen. Und wenn man das dann mit Exponentialfunktionen, ob linearisiert oder nicht, macht, wird es vermutlich noch schlimmer. Offensichtlich kommt bei der linearen Regression des linearisierten, exponentiellen Zusammenhangs das Gleiche bei raus, wie bei der direkten, exponentiellen Regression (ist das intern vielleicht das Gleiche?). Aber ein tolles Bestimmtheitsmaß bedeutet noch lange nicht, dass nicht irgendwo ein Fehler sein kann, der eigentlich groß war und dann klein logarithmiert wurde.

Xyrofl hat geschrieben:Es ist schon bei Geraden nicht richtig, von dem Bestimmtheitsmaß auf den Regressionsfehler und die Genauigkeit schließen zu wollen. Und wenn man das dann mit Exponentialfunktionen, ob linearisiert oder nicht, macht, wird es vermutlich noch schlimmer.

Naja. Wenn das R² groß ist und trotzdem Fehler gemacht wurden, dann wurden sie wenigstens konsequent - also wiederum genau - gemacht. Wenn er z.B. fälschlicherweise immer 10 % länger gewartet hat, entspricht die Kurve zwar nicht der Realität, aber das R² wäre genauso groß. Meinst du das? Das wäre ja noch verschmerzbar. Aber wenn es Außreißer gibt, wo man mal gepennt hat, dann wird das R² deutlich kleiner sein. Also irgendwie ist das schon ein Anhaltspunkt für ein genaues Arbeiten.

Ne das meine ich nicht. Das R² ist einfach so ein Zahl die stumpf daher kommt zu voreiligen Schlüssen verleitet. Ich hatte schon genug Geraden, wo zwar das R² gut war, aber der Fehler dann für die Analyse trotzdem nicht klein genug war. Man bräuchte solche Größen, wie den Regesssionsfehler.
Das R² soll angeben, wie sicher der gewählte Zusammenhang im Rahmen der Korrelationsanalyse der richtige ist, also beantwortet es die Frage "Ist das ein linearer Zusammenhang?", aber nicht die Frage "Wie genau ist das?".

Für eine Analyse bringt einem das dann nicht mehr so viel. Und wenn ich kleine Fehler in der Geraden habe, aber dann wird potenziert, dann sind das hinterher vielleicht sogar riesige Fehler. Beispielsweise eine Abweichung zwischen pH 6 oder pH7, das mag klein wirken, ja nur ein pH-Punkt, aber das ist hinterher eine Größenordung in der Konzentration wenn man potenziert. Das nennt man schlecht konditioniert, wenn Fehler explodieren.

Bestes Beispiel: Mach die Gerade einfach 10mal länger als du sie brauchst (sofern der lineare Bereich so groß ist) und dann ist bei gleicher Genauigkeit das Bestimmtheitsmaß viel besser, weil die Fehler sich auf eine viel größere Gerade verteilen. Genauer wird dadurch nichts.

@Pok und Xyrofl: Danke für die Erstellung der Kurven! Den ersten und letzten Wert habe ich in der Tat geschätzt nach der Formel: 0,25 mM konzentrationsabnahme = doppelte Zeit, so wie ich es für die drei Werte 1,0-0,5 mM gemessen hatte. Natürlich ist das ein ganz subjektives Ergebnis und steht Verzerrungen durch Erwartungen offen. Aber ganz sicher ist, daß die Zeit nicht linear mit der Konzentration ansteigt. Ich wusste nur nicht, wie ich es mathematisch formulieren sollte (dabei isses so einfach ).

Wenn ich meinen Leitungswasser-Messwert in deine schöne Geradengleichung einsetze, Xyrofl, bekomme ich 0,87 mM heraus - fast dasselbe wie ich in meiner Kurve abgelesen habe.

Ich bin von einer Reaktion erster Ordnung ausgegangen, weil ich folgendermaßen überlegt habe: die Konzentration an Ba²⁺ ist praktisch konstant hoch verglichen mit den doch niedrigen Sulfatkonzentrationen (25 mM im Vgl zu max 0,5 mM Sulfat im Ansatz) und damit hängt die Zeit bis zur Trübung (i.e. bis eine bestimmte Menge an BaSO₄ - nämlich die eben sichtbare - gebildet wurde, nur von c(SO₄) ab. Das gäbe dann ein Konzentrations-Zeit-Gesetz erster Ordnung. Oder mache ich einen Denkfehler (was mich nicht übermäßig verwundern würde)?

Wie schön, daß ich hier meine Kenntnisse in Reaktionskinetik auffrischen kann!

Die "komplizierte" Reaktionsgleichung habe ich ergänzt - ob ich doch einen Artikel daraus machen soll? (die Diskussion ist eigentlich noch interessanter als das Experiment)

lemmi hat geschrieben:Ich bin von einer Reaktion erster Ordnung ausgegangen, weil [...] damit hängt die Zeit bis zur Trübung [...] nur von c(SO₄) ab.

Ich glaube hier ist die Antwort: "Viele Reaktionen 2. Ordnung lassen sich nämlich wegen des Überschusses eines Reaktionspartners in Reaktionen 1. Ordnung umwandeln." (andere Quelle)

Es ist also eine Reaktion pseudo 1. Ordnung.

Ja, das habe ich inzwischen beim Stöbern in meinen Büchern auch gefunden. Ein bissel intuitives Wissen über Kinetik ist noch übrig geblieben...

Mir fehlt noch ein "aha-Erlebhnis", vielleicht kannst du mir da helfen, @Xyrofl? Wie hängt die Reaktionsgeschwindigkeit mit der Proportionalität von Konzentration und ln 1/t zusammen? Kann man deine Gerade aus dem Geschwindigkeitsgesetz ableiten?

Ist es egal ob man die logarithmische Gleichung mit dem lnt (bzw ln1/t) oder mit dem ln[SO₄^2-] bildet? Man könnte ja auch die koordinaten vertauschen und [SO₄^2-] als von t abhängige Variable auftragen. Etwa so:

ln1/[SO₄^2-] ~ t

bzw. :

-ln[SO₄^2-] = kt + c

geht das auch?

Wie hängt die Reaktionsgeschwindigkeit mit der Proportionalität von Konzentration und ln 1/t zusammen? Kann man deine Gerade aus dem Geschwindigkeitsgesetz ableiten?

Ich habe als Näherung angenommen, dass die Konzentrationen näherungsweise konstant bleiben, weil die Stoffmenge, die der Niederschlag bei beginnender Trübung besitzt gering gegenüber den anderen Stoffmengen ist. ( Diese Näherung wird im Folgenden I genannt)

Dann haben wir also nach I eine konstante Reaktionsgeschwindigkeit, die von den Startkonzentrationen abhängt, genauer von der Sulfatkonzentration (alles andere ist ja konstant und wird zu einem Paramter, der uns nicht weiter interessiert). Die Sulfatkonzentration nenne ich im Folgenden [A]. Die Reaktionszeit, bis der Niederschlag sichtbar wird ist aus trivialen Überlegungen heraus invers zur Reaktionsgeschwindigkeit. Je schneller es reagiert, desto weniger muss man warten.

Das t ist hier die Wartezeit und somit etwas ganz anderes als das t in den Zeitgesetzen, wo man die Konzentration als Funktion der Zeit darstellen kann. Für sowas müsste man die Konzentration mit einem Sensor die ganze Zeit über ständig messen, was wir hier aber nicht tun. Dann wäre v=d[A]/dt. Hier ist aber t die Wartezeit und deswegen gilt: v ~ 1/t.

Nun können wir vermuten, dass wie bei einer Reaktion erster Ordnung v~[A] sein könnte. Dann wäre mit v~1/t also [A]~1/t. Das ist hier aber nicht der Fall, eine solche Auftragung sieht aus wie Kraut und Rüben. Man könnte vermuten, das läge an der oben eingeführten Näherung I. Ich habe das einmal ausgerechnet und es ist nicht der Fall. Die Rechnung war lästig und nutzlos und ich habe sie verlegt, wenn du willst, mache ich das neu, aber es ist eigentlich überflüssig.

Meine zweite Vermutung war, dass es gar keine Reaktion 1.Ordnung ist, sondern eine ganz andere Sache. Ich habe einfach mal vermutet, dass die Reaktionsgeschwindigkeit irgendwie exponentiell von der Konzentration abhängt, weil ich glaube, dass das für die Nukleationsrate gilt. Also v~exp(b*[A]). Dann logarithmieren wir und bekommen:

ln(v)~b*[A], wobei natürlich alle linearen Funktionen gleich skalieren, wesshalb also auch

ln(v)~[A] gilt, da wir ja wissen, wie die Wartezeit t mit der Reaktionsgeschwindigkeit zusammenhängt, können wir auch schreiben:

ln(1/t)~[A], das ist die Auftragung, die ich benutzt habe.

geht das auch?

Natürlich geht das nicht, man kann nicht einfach die Variablen vertauschen, du müsstest mittels Äquivalenzumformungen nach t umstellen, wie bei anderen Gleichungen auch.

erstmal Danke für deine Ausführungen!

soweit ich mich erinnere folgen exponetielle Wachstumsvorgänge vom Stil: in einer gewissen Zeiteinheit verdoppelt sich Y (z.B. das Wachstum einer Bakterienpopulation - alle 30 Minuten vedoppelt sich die anzahl der Organismen) einer e-Funktion. Kann man das hier aus den (zugegebenermassen spärlichen) Messwerten nicht direkt ablesen (alle 0,25 mM Sulfat verdoppelt sich die Zeit bis zur Trübung)?

Natürlich geht das nicht, man kann nicht einfach die Variablen vertauschen, du müsstest mittels Äquivalenzumformungen nach t umstellen, wie bei anderen Gleichungen auch.

wie sähe so eine Äquivalenzumformung aus?

wie sähe so eine Äquivalenzumformung aus?

Ich glaube jetzt habe ich dich verwirrt, ich meine ganz normale Termumformung, wie bei normalen Gleichungen oder Ungleichungen. Einfach auf beiden Seiten das Gleiche machen. Ob da ein Gleichheitszeichen steht oder ein Ungleichheitszeichen oder ein Proportionalitätszeichen ist fast egal. Nur musst du hier aufpassen, dass es ein paar Besonderheiten gibt.

x ~ b*x Ist korrekt, alle linearen Funktionen skalieren gleich.

exp(x) ~ exp(b*x) ist nicht korrekt

Kann man das hier aus den (zugegebenermassen spärlichen) Messwerten nicht direkt ablesen (alle 0,25 mM Sulfat verdoppelt sich die Zeit bis zur Trübung)?

Natürlich kann man das, man kann es ganz einfach aus der Regressionsfunktion ablesen, wie bei ungebremsten Wachstumsprozessen auch. Wenn man die Regressionsfunktion hat, kann einem die Zahl der Stützpunkte ja egal sein, das beeinflusst die Genauigkeit, aber nicht die Auswertbarkeit. Zwei würden ausreichen, wenn man weiß, dass es exponentiell ist (wir haben zwei Parameter).
Ich finde aber, dass das hier eher verwirrt. Es sind die gleichen mathematischen Funktionen, bzw. mit unterschiedlichem Vorzeichen im Exponenten, also das Gleiche wie eine Zerfallsfunktion, aber ob die Warte-Zeit auf der Skala der Konzentrationen zerfällt, wie ein Radionuklid auf der Zeitskala? Das wäre eine merkwürdige Vorstellung...

Xyrofl hat geschrieben:Ich glaube jetzt habe ich dich verwirrt, ich meine ganz normale Termumformung, wie bei normalen Gleichungen oder Ungleichungen. Einfach auf beiden Seiten das Gleiche machen. Ob da ein Gleichheitszeichen steht oder ein Ungleichheitszeichen oder ein Proportionalitätszeichen ist fast egal. Nur musst du hier aufpassen, dass es ein paar Besonderheiten gibt.

x ~ b*x Ist korrekt, alle linearen Funktionen skalieren gleich.

exp(x) ~ exp(b*x) ist nicht korrekt

Ja, die Verwirrung war auf das Wort "Äquivalenz" zurückzuführen. Nach c(SO₄^2-) auflösen ist ja einfach.
Aber dein Beispeil verwirrt mich erneut... Was bedeutet der *? Exponent oder Multiplikation?

Xyrofl hat geschrieben:... Es sind die gleichen mathematischen Funktionen, bzw. mit unterschiedlichem Vorzeichen im Exponenten, also das Gleiche wie eine Zerfallsfunktion, aber ob die Warte-Zeit auf der Skala der Konzentrationen zerfällt, wie ein Radionuklid auf der Zeitskala? Das wäre eine merkwürdige Vorstellung...

Das finde ich eine lustige Analogie! Dann gibt es also eine Halbwertskonzentration der Wartezeit!

Sag mal - aber wenn du das als Gerade darstellst schneidet diese doch irgendwann die y-Achse bei x=c(SO₄^2-)=0. Das ergäbe dann eine endliche Wartezeit bei der Sulfatkonzentration 0 während die Wartezeit doch asymptotisch gegen unendlich gehen müsste. Liegt wahrscheinlich an den Vereinfachungen in den Vorannahmen, oder?